
My neighbor likes to ask big questions about big ideas. He’s not pretentious and doesn’t pontificate, so I think he just likes big questions. Anyway, the other day he asked what the necessary components of an ideal public education were. “Writing,” I said, naturally. He agreed partly because, he said, good writing involves good thinking. That’s certainly true, at least of good nonfiction writing. I’m less interested in big questions, though, and I didn’t take it any further – into, for instance, whatever “good thinking” might be.
Then at the coffee shop: Grace and Larry were arguing about the violence in Ferguson, Missouri. Larry said what you always hear, that the conflict between the police and the community was because the police force was white and the community was black. Grace said, “those two facts are not necessarily related,” and pointed out that Baltimore (where we all were) had its Freddy Grey violence but the police force and community, not to mention the city council, are pretty much the same mix of black and white. This is not quite true: Baltimore is 28 percent white; its police force is 45 percent white. But Grace’s point was that Larry wasn’t being logical, that he was committing a logical fallacy.
That is, he assumed that the tension between police and community is determined by the racial mix of each, and that Ferguson’s police force and community had different racial mixes, and so Ferguson had tension. The logical fallacies are all named, oh joy! I think, but am not sure, that this is the logical fallacy of begging the question, petitio principii: “a conclusion is derived from premises that presuppose the conclusion, ” or you try to prove a thing by assuming it’s true.
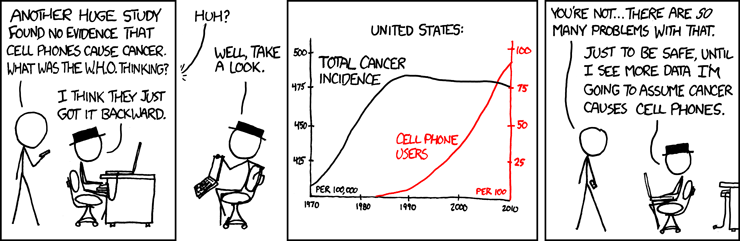
I have a pure and deep love of logical fallacies, though they’re complicated, usually explained formally, and a little hard to get my mind around. So I’m not sure exactly what they are, and I suspect I mostly like their names and maybe I get them mixed up with the religious heresies – not that I know what they are either. Bear with me. I’m getting back to my neighbor’s big question about the components of an ideal education being good thinking — and good thinking, for sure, includes avoiding the logical fallacies. Whatever they are.
Same coffee shop, same morning: Mike, a judge, was telling John that defense lawyers didn’t always like to call witnesses for alibis – e.g., “he couldn’t have done it because he was with me” – because if the jury thought the alibi witness was an unreliable liar, they assumed the defendant was also an unreliable liar and tended to convict. Mike called it “burden shifting,” which I assume means shifting the burden of proof to somebody other than the defendant.
At first I thought this might be the most beautiful logical fallacy, the tu quoque version of the ad hominem fallacy: “not accepting a view or a recommendation because the espouser him- or herself does not follow it.” Or not: tu quoque just means “you too,” as in “I know we Republicans did something bad but the Democrats did it too.” But no, that’s not quite what the jury was thinking. So maybe it’s the fallacy of the undistributed middle, which I think goes like: 1) witness and defendant are friends; 2) witness is a liar; so 3) defendant is also a liar.
I mean, that’s just: if A=B and B=C, then A=C, right? I asked Mike if, in judge school and lawyer school, he was ever taught formal logic and he thought a minute and said, “no.” I realize belatedly that Mike might have known what I’d forgotten: that “formal logic” is highly mathematical and not likely to be useful to lawyers; I shouldn’t have said “formal.” In fact, that’s what’s wrong with A=B, etc. A is something you can specifically limit, and define as equal to B. But a defendant? a witness? and the implications of friendship? No limits there, no sharp definitions, only infinite gradations of individuality. I don’t need to explain the difference between a definable A and an A who is an alibi witness who might be friends with the defendant but wouldn’t lie for him. John said it was all just common sense anyway.
I think John is right, it’s just common sense — but I think it seems like that only if you already understand the fallacies. I’d been listening to the arguments of the lawyers and politicians in the impeachment hearings, and logical fallacies were zipping around like a roomful of flies. And I wanted to barge in there and yell, Ad hominem! Petitio principii! Post hoc ergo propter hoc! (B happens after A so B is caused by A, a lot of this going around) Argumentum ad nauseam! (no explanation needed). So yes, the ideal education should include logical fallacies. And I wish I knew what they are.
Epilogue: my neighbor who likes big ideas enthusiastically lent me his copy of David Hackett Fischer’s Historians’ Fallacies, which is about exactly what the title says it’s about. I’m not going to read the whole book even though the author, for an academic, is an uncommonly lively writer. But in the introduction, he quotes a 19th century logician: “there is no such thing as a classification of the ways in which men may arrive at an error: it may be doubted that there ever can be.” Thereby undermining not only his whole book, but this post as well. There you are.
__________
Cartoons are by XKCD who is justly famous, ubiquitous, and generous enough to make all his cartoons Creative Commons.