The Last Word On Nothing

I leave today for a backpack with my two kids off the North Rim of the Grand Canyon. Per our usual, we are going without maps, compass, gps, or a trail. This is how we do it together, traveling by line of sight, letting geography show us the way out and back.

I used to come here with the now late George Steck, a pioneer Grand Canyon route-finder and a theoretical mathematician who worked at Sandia Labs in New Mexico. Without trails, we’d climb  layer by layer through the canyon, reading stone like sheet music, lowering and raising our packs on ropes. The maps we carried were in our minds, topographic contours fitting into the convolutions of our brains. It’s how our species has moved for most of its evolution. Our map was always 1:1.

In his 70s, George moved slowly. Not painfully, just slowly. He took rests, palms spread on his thighs, the antiquated frame pack shoving at his old back. He used aluminum poles to help his balance. They clicked as they touched the next solid rock down.

I often trailed him with my notebook, catching bits of his wisdom, sketching his words, his replies to my questions.

“Why do you do this? Wandering around such a challenging place?”

“I like it.”

“But why here? Why such a unique task?”

“It’s not unique. I just put one foot in front of the other.”

“That’s not what I’m asking…why do you walk for 80 days and find satisfaction with some boulder-filled chute that gets you from one place to the next? It must not have been a common hobby among people at the lab.”

He always answered with humility, even though he sensed the answer I was trying to find, a connection between math and canyons. He didn’t like to mix work and pleasure. For him, the Grand Canyon was refuge. He could throw his mind into this web and it said back to him: stone, wind, stars, river.

“Why George?”

“Because, I want to, Craig. Same for you, right? We are driven by what we want.”

At the Sandia Laboratory, George had worked with the mathematical principles of low-flying aircraft, delving into his postulations the same way astronomers explore black holes, the way physicists play with leptons and quarks, mostly with numbers. His conclusions were reached with logic, pages and books and tomes of logic. He  told me, “I found a very simple, beautiful formula for some very complicated expressions.”

When he talked about math could have just as easily been talking about his time in the wilderness, hundreds of days stacked up looking for ways through cliffs and towering tributaries. Twice he walked the Grand Canyon end to end, almost 400 miles of questions and decisions.

My hypothesis about George is that his routes were theorems. The pages of equations that he wrote were handholds, boulders, and cracks. He had starting places and destinations, and his body found the way between. All that hullabaloo of canyons came down to the perfect answer to the equation.

He once gave to me some of his scientific work published in a journal of mathematics. When I read the material, my eyesight blurred in all the pages of formulas, letters, numbers, and symbols. The only thing I could decipher was that George’s mind was witness to something vast.

The papers were part of what he called his First Great Epiphany, a mathematical discovery he considered epic. Here’s the theorem:

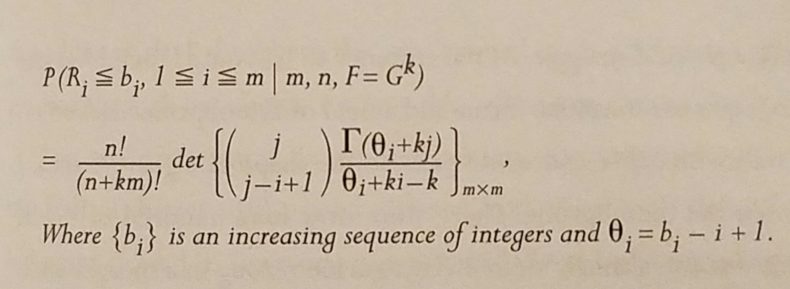
I ran my finger across the formula when I saw it, trying to find its intention, seeing only a meaningless jumble. But I knew there was meaning, like the lists of geologic names in the Grand Canyon, enough meaning to bring George fame among his peers worldwide. He spent the next five pages proving this theorem true. To prove something like this true is a breakthrough, revealing a path of logic never before utilized, putting a first stroke of human knowledge on paper. He had found a route.

Equally, his routes in the Grand Canyon brought him fame among his peers. He had followers, like me, learning from him as he led us into these shadowy labyrinths.

The last time we were together, a couple years before he died, George was 77. We were packing a loop from rim to river and back to rim, no trails, no signs. He had done it decades earlier and remembered his decisions. The map was at his feet.

Sitting in the shade of a shell-shaped canyon, George finally told me that I was right. He said that math and the Grand Canyon were the same. His life was a search for a way from here to there through some of the most complex terrain possible. He was made for this, however it manifest.

That was our last time together. Now I return with my children. We will load up backpacks and carry them to the edge. We will not have a trailhead, a sign, nothing to mark our entrance. From there on we will write equations with our feet and hands, just like George wanted.

George P. Steck 1925-2004

Top image: shutterstock